Что если поискать модель от весов (другой модели) к её лоссу, ну или к скору?

Вообще, изначально идея была в другом. Вот в топологическом анализе данных растят шары из каждой точки данных, и анализируют число компонент связности (получают persistence diagrams).

Что если данные это веса сетки, одномерные такие вот точки, а диаграммы дают какую-то информацию про качество сетки?

Ответ: дают больше, чем сами веса.

def make_data(iterations=10000):
    units = []
    scores = []
    for index in tqdm.tqdm(range(iterations)):
        np.random.seed(index)
        random_x = np.random.normal(size=X.shape)
        random_y = np.random.randint(0, 2, size=y.shape)
        classifier = MLPClassifier([10, 10], max_iter=1, random_state=index).fit(random_x, random_y)
        current = []
        for layer in range(len(classifier.coefs_)):
            current += classifier.coefs_[layer].flatten().tolist() + classifier.intercepts_[layer].tolist()
        score = classifier.score(X, y)
        scores.append(score)
        units.append(current)

    return np.array(units).reshape(iterations, -1), np.array(scores)

где X, y — это например two moons dataset.

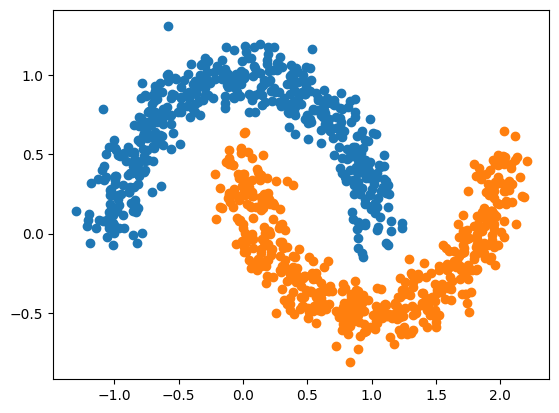
К слову, MLPClassifier([10, 10]) из scikit-learn выдаёт > 0.99 на трэйне и тесте. Ну а mean cross val score от весов напрямую к скору даёт… R2 -0.349.

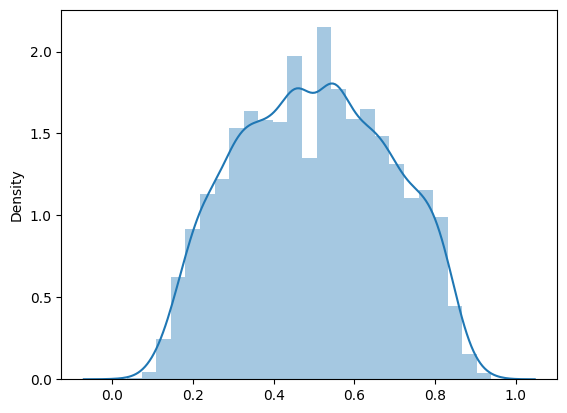
Здесь выкинуты скоры между 0.49 и 0.51. Так как их процентов 70. А если взять диаграммы:

def get_diagrams(points):
    rips = ripser.Rips(maxdim=1, verbose=False)
    dgm = rips.fit_transform(points)[0]
    dgm = dgm[:-1][:, 1]
    if len(dgm) < len(points) - 1:
        dgm = np.array([0] * (len(points) - len(dgm) - 1) + dgm.tolist())
    return dgm

… то тогда регрессия от диаграмм к скору даёт на кроссвалидации R2 -0.003. Считай, средним предсказывает. Уже лучше.

Поэтому это и слабое подозрение. А что важно заметить, процедура рандомного «весования» сетки для two moons дала внезапно accuracy 0.94 в 1 из 10 тысяч случаев. Вот это интересно, конечно.

Ну а топология здесь причем… а при том что малые шевеления весов не должны менять классификацию серьезно. А эти малые шевеления и выражаются в компонентах связности.

А изначально думалось, что можно построить пошаговый оптимизатор, который бы брал (какую-то или) самую большую компоненту связности для весов и усреднял бы веса в ней итеративно. То есть без дифференцирования. Но что-то не задалось сегодня. Может быть, когда-нибудь, кто знает. А может и нет 🙂