Давным-давно…

Скачивал я кучу данных статистики ДТП по РФ за разные лохматые года, и вывел какую-то формулу (непонятно зачем) зависимости фазы луны (а точнее процента её видимости) и количества участников в ДТП за сутки.

Данные не нашел у себя… долго помню их склеивал. Но внезапно вырезочку всё же заобнаружил. В этом туториале от Яндекса, шаг 1 пункт 1. Это те самые данные, на которых надуманная формула всё же сработала.

Формула

$$ X = \ln { \frac {1} {\arccos {V} } } $$

Собственно V — это процент видимости луны в дату. Выглядит вот так.

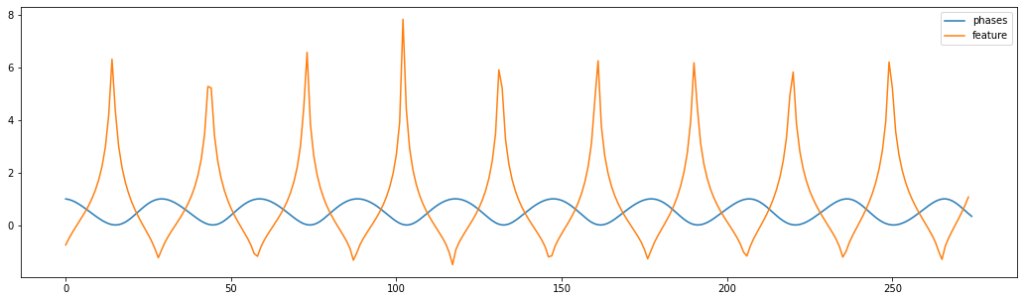
А теперь — как выглядит наш таргет (число участников ДТП в сутки).

Напрямую зависит не Y от X, а чуть помутнее — масштабированные разницы таргета от масштабированного признака (оранжевого).

Phase — это преобразованная фаза, Value — это масштабированные разницы, а вот Target — это такая вещь:

$$ T = e^{ 2 \frac {P — V} {P + V}} $$

И вот этот вот таргет…

Прогнозируется, линейкой, а потом KNN (N=1).

Линейка показывает R2 порядка 0.87-0.94 на пяти фолдах.

Если проворачивать фарш обратно, вечер перестаёт быть томным.

Так вот, я к чему всё это

1. Переход в бездрейфовое пространство, аналогия в нем, и выход — это работает.
2. То что неплохо прогнозируется в бездрейфовом — может плохо прогнозироваться в оригинальном — процедура перехода туда и обратно может выбросить интересное и снаружи и внутри.

То есть малое смещение (bias) в бездрейфовом, должно сочетаться еще и малой вариабельностью (variance) там же.

Для решения любой задачи прогнозирования недостаточно экстраполяции, нужна еще креативность (выбора пространства)

С этими же двумя ингридиентами под силу всё