В поисках алгебраической структуры data generation process

Началось всё безобидно. Что если взять все разницы между точками датасета (вместе с таргетом), и эти разницы рассмотреть как элементы группы? То есть пути между точками.

Группа сама по себе абелева, но не все слова группы лежат на многообразии. Вообще говоря, надо рассматривать перестановки путей, но они не коммутируют, а чтобы сделать их абелевыми, надо рассмотреть левый смежный класс с коммутантами. И тогда можно построить трансформер (или RNN — тоже Тьюринг-полная сетка), который по словам коммутирующих перестановок путей научится генерировать точки на многообразии. А чтобы решить, лежит ли точка на многообразии или нет — достаточно будет проверить целочисленность решения задачи линейного программирования.

Но слишком много надо насчитывать объектов.

Просто посмотрим

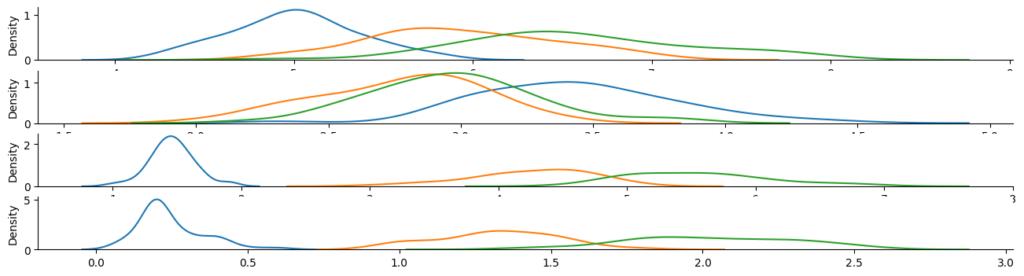
Возьмем датасет Ирисы Фишера, и выкинем из него одну координату.

onehot = OneHotEncoder(sparse_output=False)

X, y = shuffle(*load_iris(return_X_y=True), random_state=1)
X = np.column_stack([X, onehot.fit_transform(y.reshape(-1, 1))]) 

from warnings import filterwarnings
filterwarnings('ignore')

figure, axes = plt.subplots(4, 1, figsize=(16, 4))
for axis in range(4):
    for color in [0, 1, 2]:
        sns.distplot(X[y == color, axis], hist=False, ax=axes[axis]);
sns.despine()

features = list(range(X.shape[1]))
features.remove(1)
X = X[:, features]

Выкидываем первую, так как она пару сортов плохо различает.

Далее сделаем всё же класс упомянутой группы.

class Group:
    def __init__(self, X):
        self.symbols = [0]
        self.vectors = [np.zeros_like(X[0])]
        for outer in range(X.shape[0]):
            for inner in range(X.shape[0]):
                if outer != inner:
                    self.symbols += [self.symbols[-1] + 1]
                    self.vectors += [X[outer] - X[inner]]
    
    def __len__(self):
        return len(self.symbols)
    
    def compute_word(self, word):
        point = np.zeros_like(self.vectors[0])
        for symbol in word:
            point += self.vectors[self.symbols[symbol]]
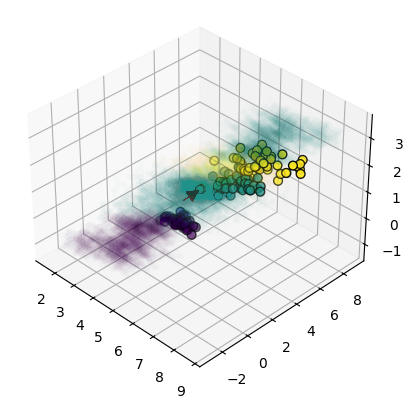
        return point

Вот так будет выглядеть (синим) результат пути [100, 8700], а цвет-класс — это результат inverse transform для one hot encoder. Он не всегда может в обратное, тогда мы считаем что точка не лежит на многообразии.