Любая поверхность без края, ну замкнутая — сфера или тор скажем — это пример многообразия. Окружность тоже многообразие. Это примеры замкнутых многообразий (пример открытого — вся плоскость или 3D).

Ниже прочитали случайно? Ничего… всё равно не то подумали наверняка 🙂

Существует гипотеза, по которой данные реальных процессов лежат на каком-то многообразии. Опровергнуть пока никто не опровергнул, а вот подтверждений тому масса.

Самолётский датасет

Я нашел обратно тот набор данных траекторий самолетов, который использовал для разговора о вложениях. Нашелся он здесь.

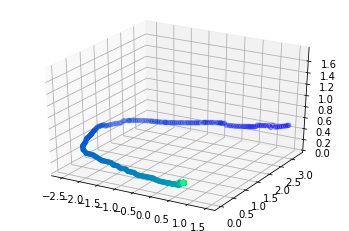
Еще вариант.

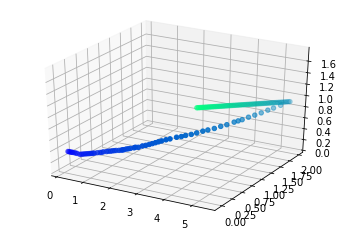
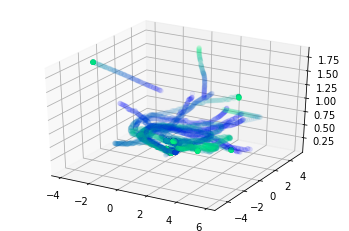
Так вот, самолёты не летают как попало, все их траектории лежат на какой-то поверхности, они не заполняют всё выделенное им пространство (вокруг аэропорта).

Данные даны же точками…

Да, данные обычно представлены в виде облака точек, а ряд алгоритмов — UMAP известный скажем — пытаются многообразие найти и даже проэксплуатировать.

Все это про топологический анализ данных, который взлетает что-то с трудом, будучи неустойчивой к шумам, но штука очень симпатичная.

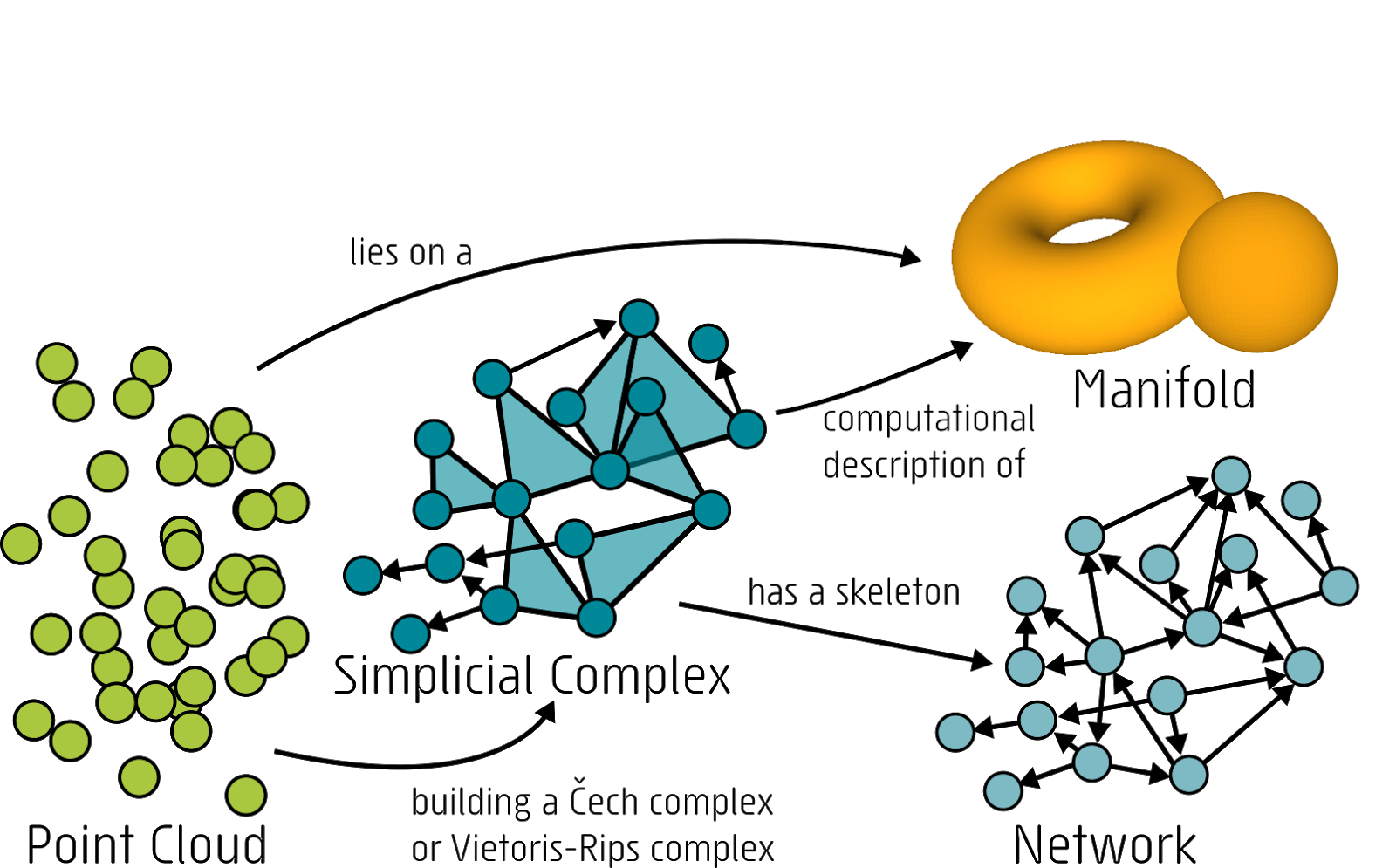
Если данные не образуют хорошей топологии, это не только потому что они шумные, а еще потому что не в то пространство вложены

SUPport Vector Machines — добавление функционально преобразованных измерений — могли бы исправить ситуацию, но без человека не способны

Нам, смертным, выход всегда один: использовать дополнительные знания (или в примитиве — данные), чтобы не ошибаться в понимании процесса.