В этот раз (даже без грязной) тетрадки. Достаточно идеи. Attention (который is all you need) для временных рядов работает по точкам. Но если закодировать куски серий — можно свести всё к классификации, или к causal language modelling — и да, я пихал биржевые индексы в (distill, fin…)gpt2. Перплексия маленькая, но токенизатор под такое не заточен — может букву пропустить, или чиселку…
Теперь к делу.
- Создается библиотека кривых из различных функций — всего у меня 8192 кривых.
- Препроцессинг (индексов) примитивный: логарифмирование, потом стандартизация.
- Кодирование — подбор наилучшей подходящей кривой по R2.
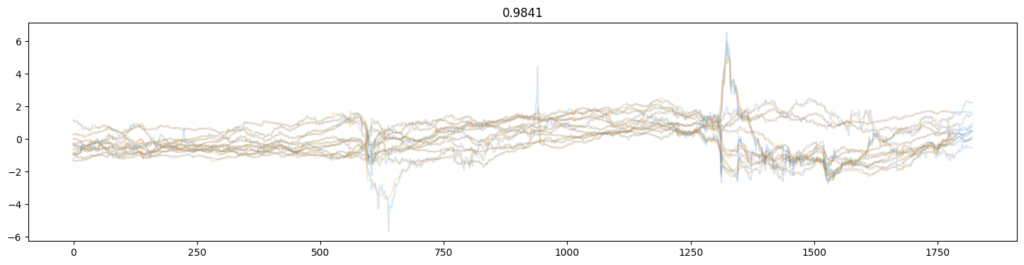
Здесь R2 на всю длину для всех — для окна 36 дней. А можно и в 7 например — там процент восстановления 99.8% (R2). Узнаете там всем известные расколбасы? 🙂
Я пихал это в ванильный (pytorch-)- трансформер, да. Сильно не парился, и результат поэтому особо не увидил. Немного cherry picking.
Перплексия на невиданном тесте 2.34. Слабовато для такой задачи как мне кажется. Можно выкруживать помощнее (данные только готовить долго).
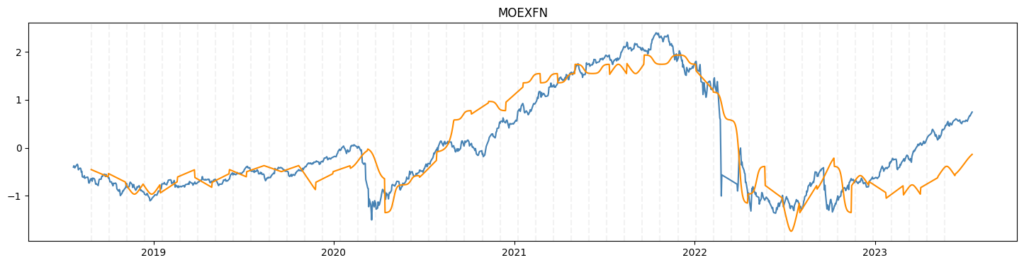
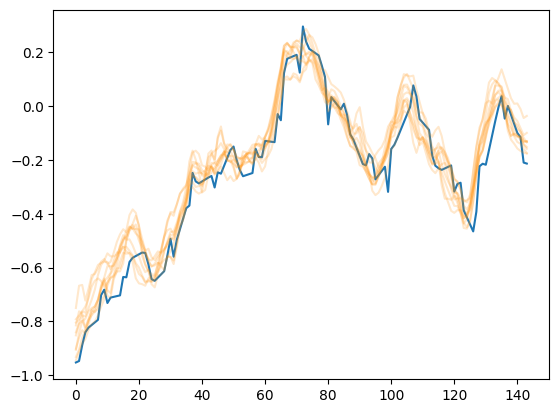
Синее на входе у ораженвого слпедующем шагом окна на выходе.
P.S. Ах да — серии пришлось поаугментировать…
P.P.S. Ах да — код. Болтовня ничего не стоит, покажите код… (с) Торвальдс.
spatial = np.linspace(-3, 3, 32)
def encode_serie(dataset, window):
space = np.linspace(spatial.min(), spatial.max(), window)
text = ""
predefined_time = False
predefined_keys = False
predefined_time = np.array([
library[key](space) for key in library
]).reshape(len(library), len(space))
predefined_keys = [
key for key in library
]
for index in range(window, (len(dataset) // window) * window, window - 1):
sliced = dataset.values[index - window:index]
word = ""
best_score = +np.inf
symbols = []
curve = sliced
scored = []
current = {}
for dimension in range(curve.shape[1]):
scores = (curve[:, dimension] - predefined_time) ** 2 / np.var(curve[:, dimension])
symbol = predefined_keys[np.argmin(scores.mean(axis=1))]
current[dimension] = symbol
scored += [scores[np.argmin(scores.mean(axis=1))]]
scored = np.max(scored)
if scored < best_score:
best_score = scored
symbols = [current[index] for index in range(curve.shape[1])]
text += "/".join(symbols) + " "
return text.strip()
def decode_serie(text, window):
result = []
space = np.linspace(spatial.min(), spatial.max(), window)
for state in text.split():
vector = []
for dimension, word in enumerate(state.split("/")):
addition = library[word](space)
vector += [(addition).tolist()]
result += [np.array(vector).T[:-1]]
result = np.row_stack(result)
return pd.DataFrame(data=result)

2 комментария на «“Subseries-as-tokens”»
Тетрадка здесь.
https://gist.github.com/timeseries-ru/f9a0e29bc8d843e0cb8a2372be067b8c
*** , чуть поясню по своим вопросам.
1. По Тьюринг-полноте. Рекуррентные и Трансформеры с PE полны по Тьюрингу, и в «моей вселенной» это не праздная история. Есть тезис Черча, о том что все интуитивно-вычислимые алгоритмы частично рекурсивные (эквивалентно реализуемые на машине Тьюринга). Вся разметка из какой-то этой истории , и модели учат программу генерации данных. Это как контекст вопроса. Потерять Тьюринг-полоноту нельзя, мы к ней все всё равно вернёмся,
2. Про теорию управления (динамическими системами). Там есть концепция передаточных функций. Преобразование Лапласа позволяет перейти в пространство деления полиномов (Лежандра они или нет — тут хз), но в целом благодаря этому преобразованию, решение динамических систем как схем — приводится к вычислениям на (гурвицевых в знаменателе, а в числителе меньшей степени для физической реализуемости) полиномов. Это в контекст почему преобразование Лапласа «интереснее»
Мы на пороге великого объединения дискретной (мат) логики и функана. Благодаря архитектурам нейросеток, которые это все окупают в продакшене).