В прошлом посте зародилось подозрение, что принятие решения (вывод) у «устройств с памятью» осуществляется путем некоторого «схлапывания» (фильтрации и агрегации) базы элементарных сюжетов.

Сейчас предложу число, которое и назову скрытый код — оно будет специфицировать оценку результата решения.

Небольшое отступление

Вообще для чего (обученные) принимающие решения (люди, кони, алгоритмы) эти самые решения принимают? Есть разные разговоры, что они противостоят хаосу — увеличивают вероятность нужных событий, — ну и в целом, они пытаются улучшить своё положение в среде.

Короче говоря, снижают энтропию. Энтропия для дискретного набора события может быть как у Шеннона:

$$ H = \sum {-p_i * ln (p_i)} $$

У Шеннона — вероятности, это вероятности символов алфавита в сообщениях. Но что если взять это как вероятности интересующих исходов ситуации, в которых этих исходов множество?

Определение

Не то, что бы меня чем-то не устраивала сама энтропия. Важно измерить энтропию «до» и «после», чтобы понять, а что собственно изменил в среде интересующий нас некий «приниматель решений».

Ну тогда получаются следующие выкладки, если взять за x вероятность исхода «до», и за y — после.

$$ С = \sum {-y_i * F_i * ln (y_i)} — $$

$$ \sum {-x_i * F_i * ln (x_i)} = $$

$$ \sum {F_i*ln (\frac {x_i ^ {x_i}} {y_i ^ {y_i}} )} = $$

$$ \sum {F_i * B(x, y)} $$

Это число C и назовем скрытый код, а числа F — фильтрами, а B — обозначение функции с логарифмом (база сюжетов).

Каждый исход имеет свой «элементарный сюжет», а их фильтрация — это некоторое, конечно, упрощение сейчас.

Функция элементарного сюжета

Функция B — достаточно своеобразная вещица, надо отметить. Стоит только посмотреть на её относительно несимметричный график.

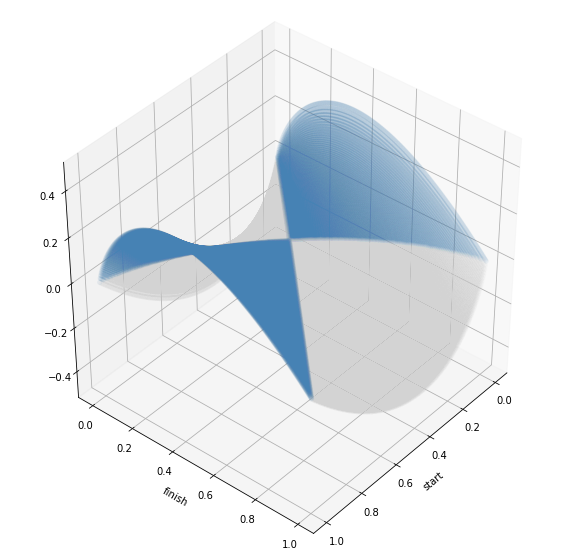
Чудес не бывает, синим — часть более нуля. Её площадь составляет менее 30% от всей площади поверхности.

Умножение на F, естественно, эту пропорцию меняет, хоть и не драматически. Скажем, если F = 1/3, то соотношение около 32.8%, а для F = 2 — оно около 28.2%.

Допустим, и что?

Вся интересность в том, что в вычислении скрытого кода участвует конечное распределение, до принятия решения неизвестное.

А это значит, что если возможно прогнозировать скрытый код — то возможно и описать принятие решений.

вычисление скрытого кода — эквивалент реализации решения

Это всё сильное утверждение, которому если и не доказательство хотелось бы найти, то хотя бы свидетельство.